Object Oriented OpenSCAD
Summary
This is a discussion on using vectors in OpenSCAD as objects that can be used polymorphically. I’ve found this to be a powerful approach which encourages more generic algorithms. It’s a bit ugly but it works. Nothing here is revolutionary but I’ve found it to be a useful way to think about the problem.
Background
OpenSCAD is a special purpose, interpreted, functional language with a limited number of built in functions. There aren’t many types and the user can’t define any.
The OpenSCAD types as of version 2021.01 are:
- float (64 bit IEEE)
- bool
- string
- range
- undef
- vector
Additionally there are modules and functions but these cannot be passed as objects. There are also lambdas but that doesn’t change anything.
Example Problem
For a project I’m working on I’m building some objects that are composed of layers carved into a block. One requirement is to be able to use more complicated shapes imported from an SVG.
In OO speak the super class is Shape with derived types SVG, Square, Circle, and None. The class Shape is abstract as there are no valid arguments, it’s like a void* in c. Each derived type differs only by the contents of the arguments vector.
Shape Definition
| Type | Member | Description |
|---|---|---|
| string | class name | |
| string | id | |
| vector [float, float, float] | position | |
| vector[arguments] | arguments |
Shape-Square Arguments Definition
| Type | Member | Description |
|---|---|---|
| vector[float, float] | size | Length, Width of square |
Shape-SVG Arguments Definition
| Type | Member | Description |
|---|---|---|
| string | file | SVG source |
Example Code
Here’s the code:
/*
Uses the dot product to sum a list
:param vector lst: vector to be sumed
:return float
*/
function sum(lst) = len(lst) == 0?
0 :
len(lst) == 1?
lst[0] :
lst * [for(i=[0:len(lst)-1]) 1];
assert(sum([]) == 0);
assert(sum([100]) == 100);
assert(sum([1,1,1,1]) == 4);
/*
Returns a subsection of a vector. Counts from 0.
:param vector lst
:param int start:
:param int end:
:return vector
*/
function partial(lst, start, end) = min(end, len(lst)) == start+1 ?
[lst[start]] : // only access a single entry
start > min(end, len(lst))-1?
[] :
[for (i=[start:min(end, len(lst))-1]) lst[i]];
assert(sum(partial([1,1,1],0,1)) == 1);
assert(sum(partial([1,1,1],0,2)) == 2);
assert(sum(partial([1,1,1],0,3)) == 3);
assert(sum(partial([1,1,1],0,100)) == 3);
assert(partial([1,1,1],1,1) == []);
assert(sum(partial([1,1,1],1,1)) == 0);
assert(sum(partial([1,1,1],1,2)) == 1);
assert(sum(partial([1,1,1],1,3)) == 2);
/*
Makes a 2D shape object
:param string shape: ID of shape
:param vector args: vector of arguments to the matching shape module.
*/
module make_shape(shape, args) {
echo(shape);
if (shape == "square") {
square(args, center=true);
} else if (shape == "circle") {
circle(d=args);
} else if(shape == "none") {
} else if(shape == "svg") {
import(args);
} else assert(0, "Unknown shape");
};
/*
Some value way larger than our largest geometry
*/
function get_infinity() = 1000;
/*
Carved block with composed of layers. All layers are cut out from their starting point to infinity.
:param vector block_size: [width, length] of block
:param vector layers: class Layer [string shape, vector[float x, float y, float layer height] position, vector arguments, string name]
*/
module make_carved_layer_stack(block_size, layers) {
layer_heights = [for (layer=layers) layer[1].z];
difference() {
total_height = sum(layer_heights);
linear_extrude(total_height, center=true)square(block_size, center=true);
for (i=[0:len(layers)-1]) {
layer = layers[i];
// first layer is only its own thickness, second is first + second ...
height = sum(partial(layer_heights,0,i))+layer[1].z;
translate([layer[1].x, layer[1].y, -height+total_height/2])
linear_extrude(get_infinity())make_shape(layer[0], layer[2][0]);
};
};
};
n_layers = 10;
layers = concat(
[["svg", [-50,-50,5], ["drawing.svg"], "stars"]],
[for(i=[1:n_layers]) ["square", [0,0,5], [[5*(n_layers-i),5*(n_layers-i)]], str("square ",i-1)]],
[["none", [0,0,10], [undef], "base"]]
);
make_carved_layer_stack(block_size=[100,100], layers=layers);
{%card%}drawing.svg layer
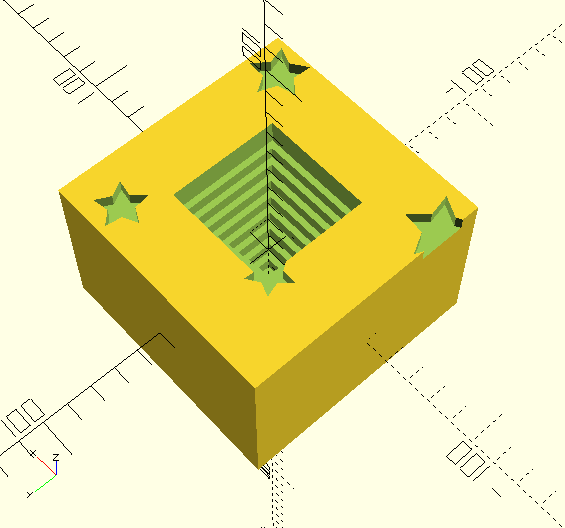
Generated object
I’m quite proud of the sum and partial functions. There’s some corner cases that are dealt with, my aim was to get them to have the same behavior as the python built-ins.
The layers can be handled polymorphically requiring only an entry in make_shape for each one with a corresponding shape module (here I’m using only built-ins for simplicity). The derived class (ish) of each shape has all its class specific members held in the arguments vector. This can be extended to make further derived classes as required.
Vectors With Named Members
Using ints for accessing members is a bit rough but functional. Key value pairs can be used if we’re getting fancy:
/* Access the field of a key value pair vector */
function dict_lookup(key, dict) = dict[search([key], dict)[0]][1];
assert(dict_lookup("name", [["name", "value"]]) == "value");
/*
Layer as a key value pair
*/
layer = [
["shape", "svg"],
["position", [-50,-50,5]],
["args", ["drawing.svg"]],
["name", "stars"]];
echo(dict_lookup(key="name", layer));
ECHO: "stars"
Structure of a Key-Value Pair Vector “Object”
Here’s an example “Class” for importing an SVG.
/*
Class SVG
string name: Class name -> "SVG"
string id
float rotation
vector[float, float, float] axis
float clearance
string file
float scale
float convexity
*/
function check_svg_object(obj) =
is_string(dict_lookup("name", obj)) &&
is_string(dict_lookup("id", obj)) &&
is_num(dict_lookup("rotation", obj)) &&
is_list(dict_lookup("axis", obj)) &&
is_string(dict_lookup("file", obj)) &&
is_num(dict_lookup("scale", obj)) &&
is_num(dict_lookup("convexity", obj)) &&
is_list(dict_lookup("center", obj));
module make_svg(arguments) {
svg = arguments[0];
assert(check_svg_object(svg));
module make_svg_(svg) {
center = dict_lookup("center", svg);
rotate(dict_lookup("rotation", svg), dict_lookup("axis", svg))
translate([-center.x, -center.y])
scale(dict_lookup("scale", svg))
import(dict_lookup("file", svg), convexity=dict_lookup("convexity", svg));
};
make_svg_(svg);
};
Each class needs to have a definition as a comment and a consistency check function. Since many functions in OpenSCAD can return undef it is a time saver to write a consistency check first. At a minimum I check all required field types. Adding an assert to check the type prevents cryptic errors from having too many sets of brackets or something similar.
There are so many settings that are required to make a design that using a dictionary and treating it as a class instance increases flexibility and cuts down on cryptic errors.
One interesting investigation for future work is how to do a derived type of a derived type in a clean and consistent manner.
